트리의 개념과 트리 순회에 대하여 알아봅시다.

이진트리의 순회(traversal)

• 순회 : 이진 트리의 모든 노드를 방문하는 일

순회를 위한 작업 3가지

1. D : 현재 노드를 방문하여 데이터를 읽는 작업
2. L : 현재 노드의 ==왼쪽== 서브트리로 이동하는 작업
3. R : 현재 노드의 ==오른쪽== 서브트리로 이동하는 작업

순회 종류 4가지 (노드 방문 순서에 따라)

• 전위 순회 (Preorder Traversal)
• 중위 순회 (Inorder Traversal)
• 후위 순회 (Postorder Traversal)
• 레벨 오더 순회(level-order Traversal)

1. 전위 순회 (Preorder Traversal)

• 현재 노드를 방문하여 데이터를 읽는 작업 D 을 가장 먼저 수행하여 DLR 의 순서로 순회하는 방법

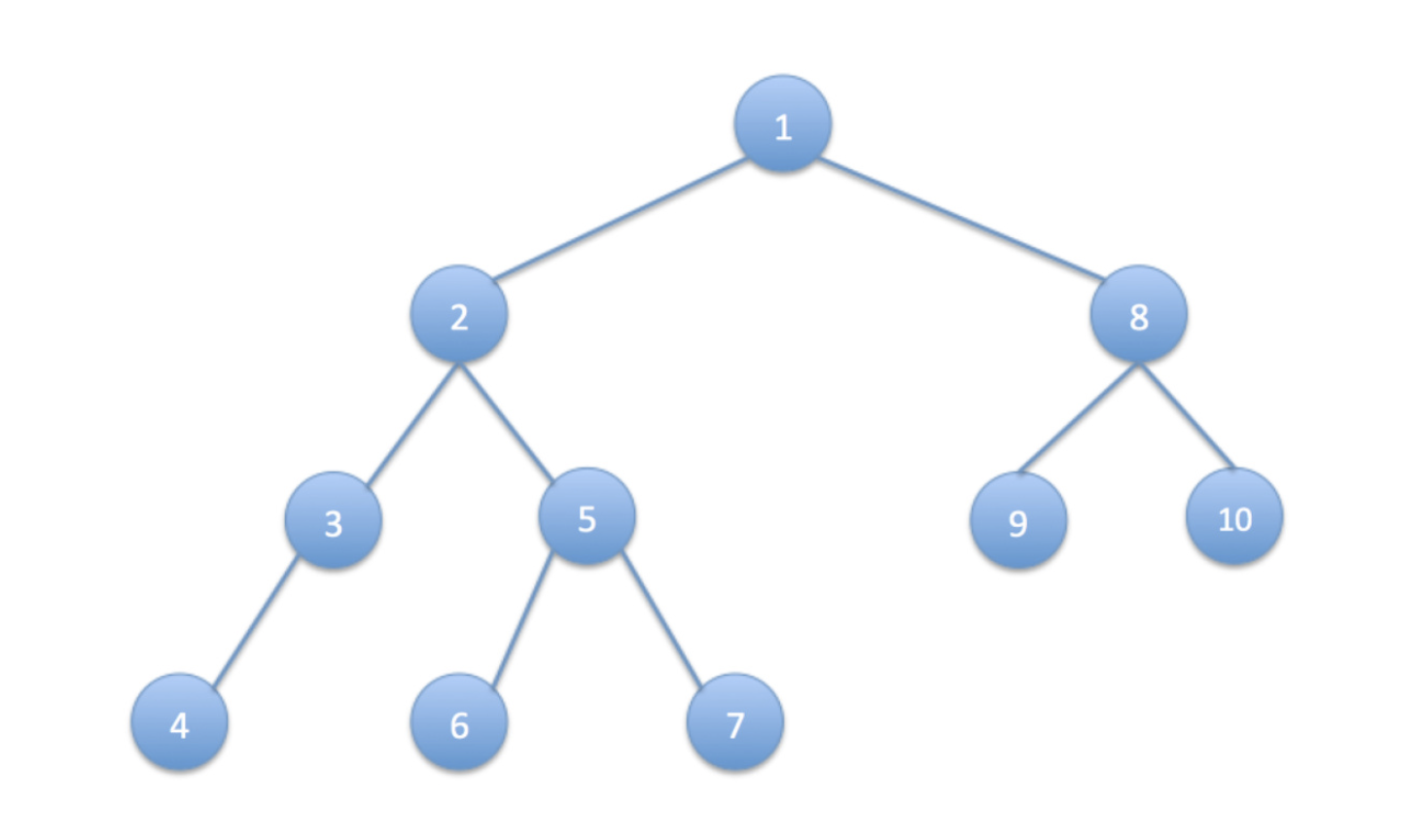
PREORDER-TREE-WALK(x)
  if x != NIL
  	print key[x] // D
  	PREORDER-TREE-WALK(left[x])  // L
  	PREORDER-TREE-WALK(right[x]) // R

2. 중위 순회 (Inorder Traversal)

• 현재 노드를 방문하여 데이터를 읽는 작업 D 을 L과 R의 사이에 수행하여 LDR 의 순서로 순회하는 방법

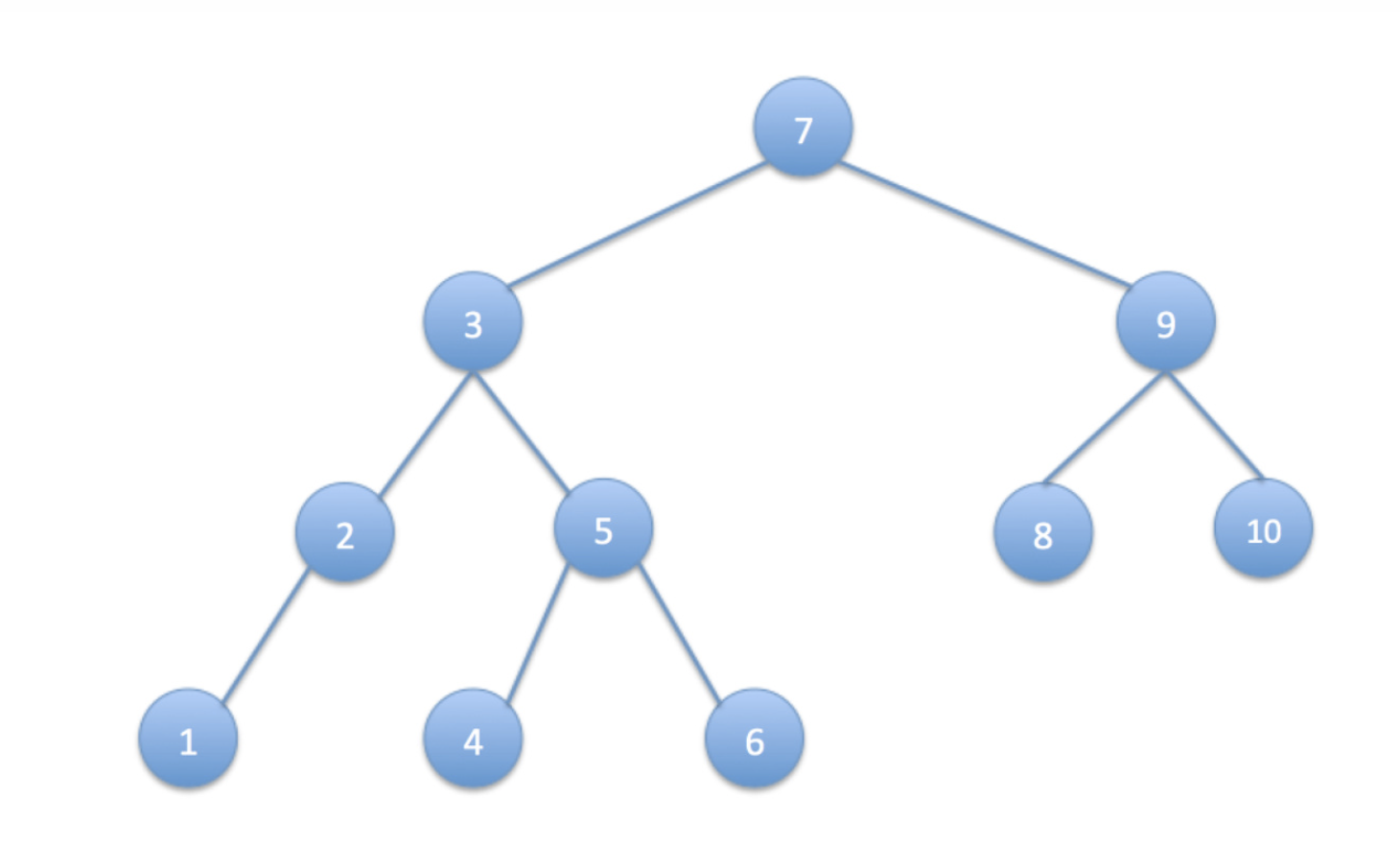
INORDER-TREE-WALK(x)
  if x != NIL
  	INORDER-TREE-WALK(left[x])  // L
  	print key[x] // D
  	INORDER-TREE-WALK(right[x]) // R

3. 후위 순회 (Postorder Traversal)

• 현재 노드를 방문하여 데이터를 읽는 작업 D 을 가장 나중에 수행하여 LRD 의 순서로 순회하는 방법

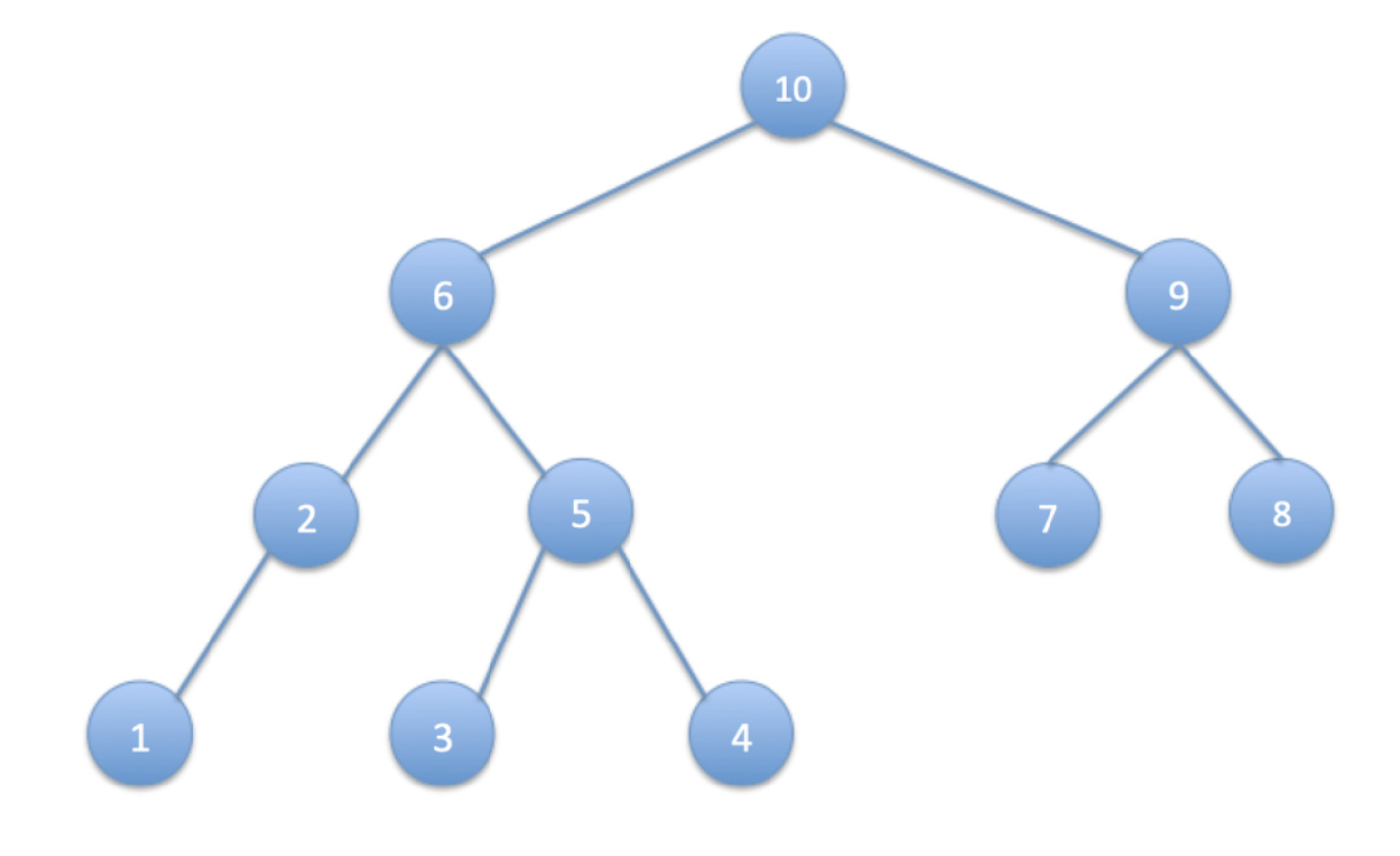
POSTORDER-TREE-WALK(x)
  if x != NIL
  	PREORDER-TREE-WALK(left[x])  // L
  	PREORDER-TREE-WALK(right[x]) // R
  	print key[x] // D

4. 레벨 오더 순회(level-order Traversal)

• 레벨 순으로 방문, 동일 레벨에서는 왼쪽에서 오른쪽 순서로
• 큐(queue)를 이용하여 구현

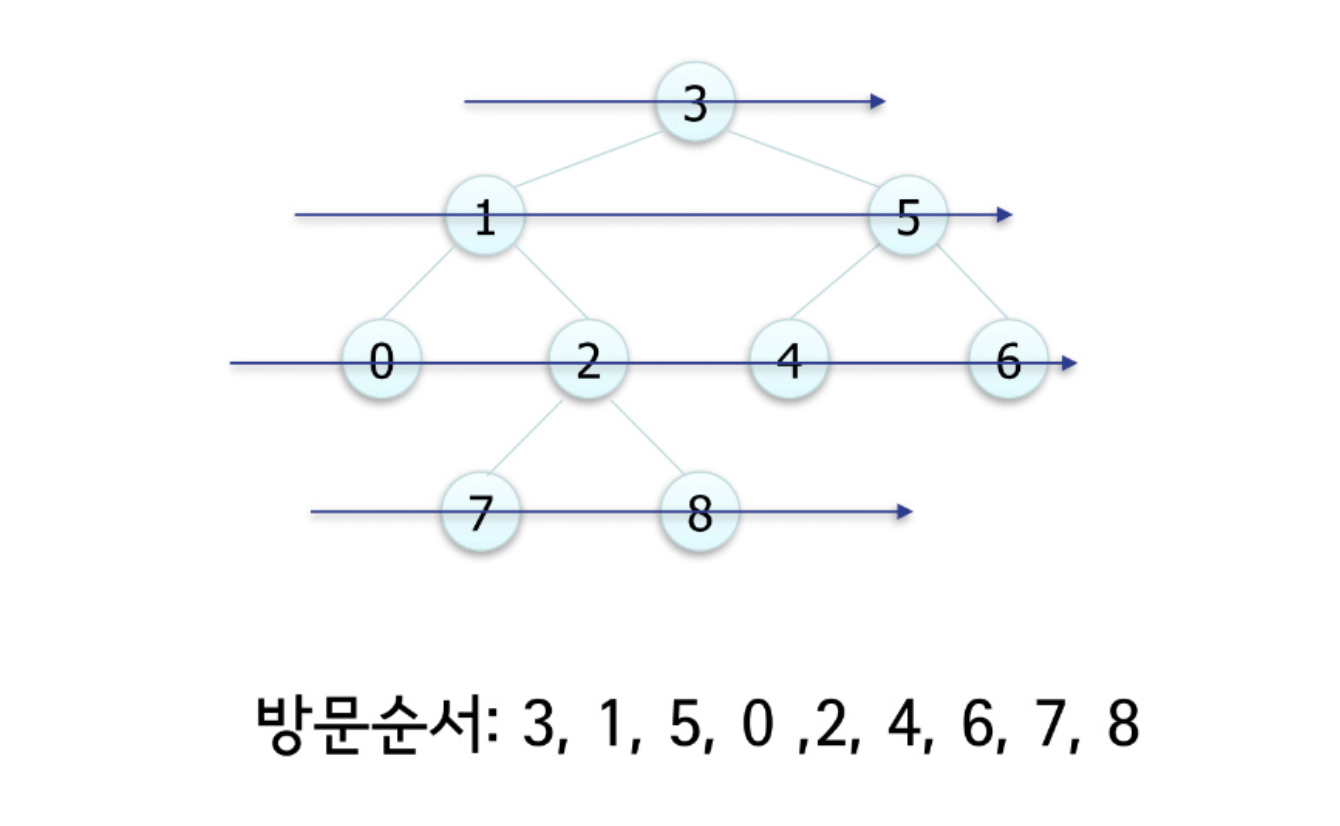
LEVEL-ORDER-TREE-TRAVERSAL()
​	visit the root:
​	Q <- root	//Q is a queue
​	while Q is not empty do
   		v <- dequeue(Q);
​    	visit children of v;
​    	enqueue childrenn of v into Q;

❗️문제

• 전위, 중위, 후위, 레벨 오더 순회 경로 구하기

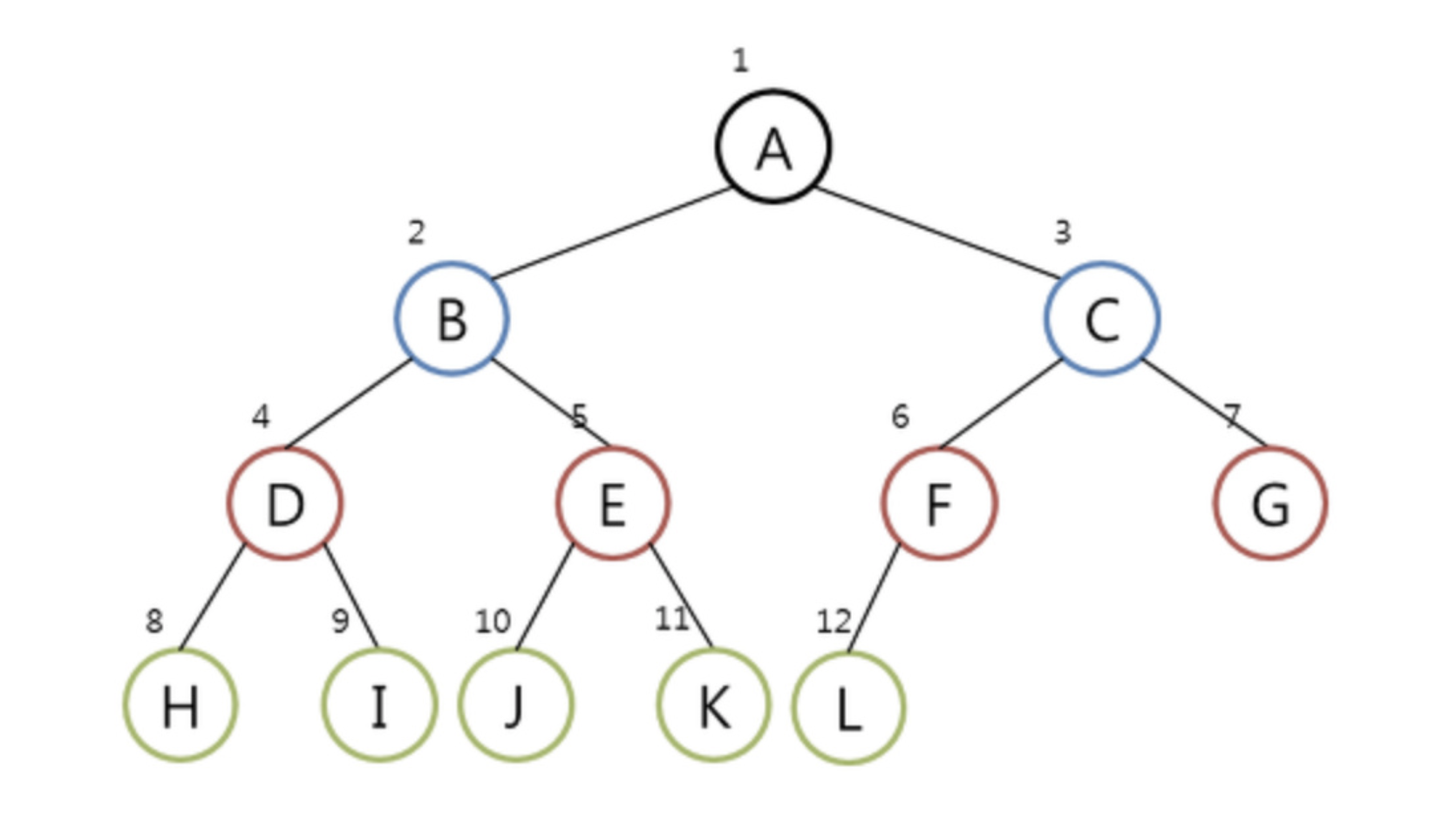
답