트리의 개념과 용어를 정리해봅시다.

트리(Tree)

(1) 트리(Tree)

1) 개념

• 계층적인 구조를 표현
  • 조직도
  • 디렉토리와 서브디렉토리 구조
  • 가계도
• 트리는 노드(node)들과 노드들을 연결하는 링크(link)들로 구성됨

2) 용어

• 루트 노드(root node) : 부모가 없는 노드. 트리는 하나의 루트 노드만을 가진다.
• 단말 노드(leaf node) : 자식이 없는 노드이다.
• 내부(internal) 노드 : 리프 노드가 아닌 노드.
• 링크(link) : 노드를 연결하는 선 (edge, branch 라고도 부름).
• 형제(sibling) : 같은 부모를 가지는 노드.

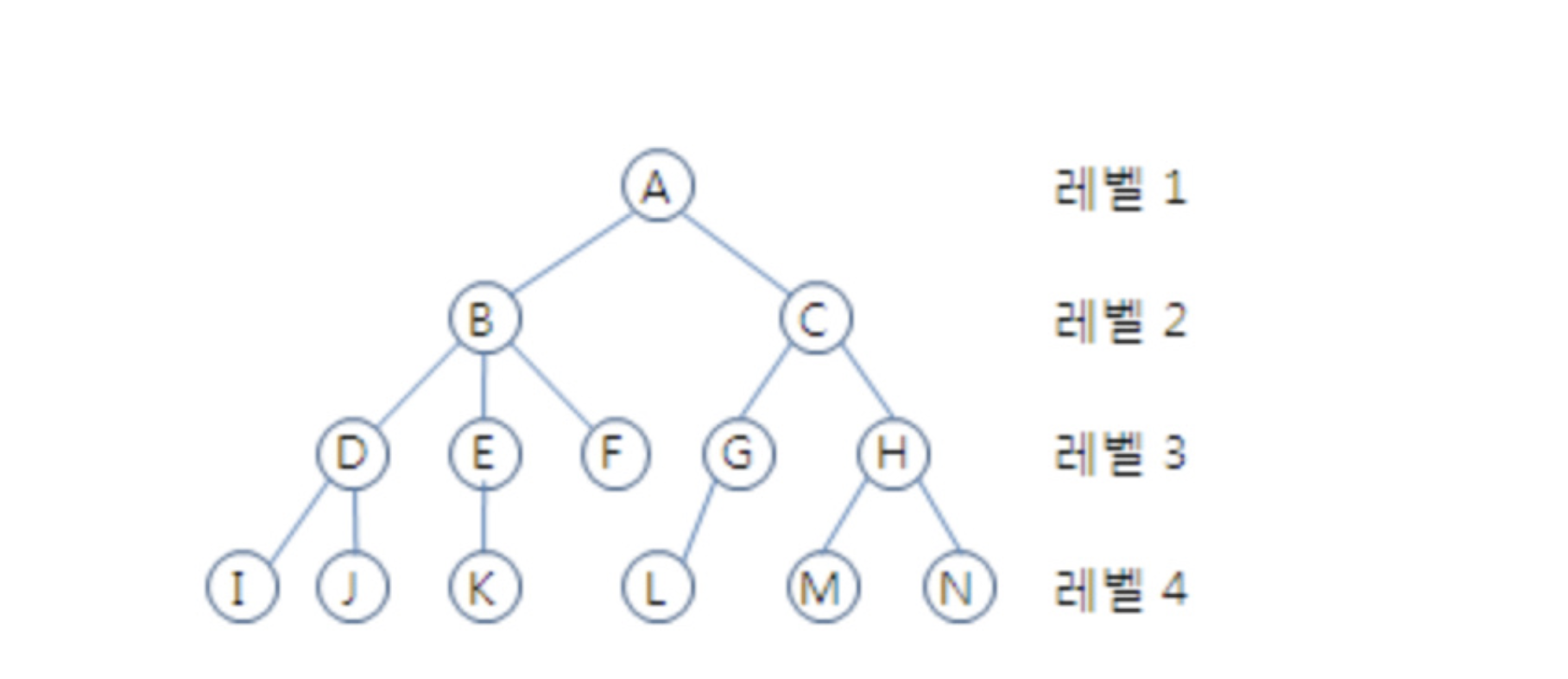
• 노드의 크기(size) : 자신을 포함한 모든 자손 노드의 개수.
  • C의 크기 : 6
• 노드의 깊이(depth) : 루트에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수
  • D의 깊이 : 2
  • L의 깊이 : 3
• 노드의 레벨(level) : 트리의 특정 깊이를 가지는 노드의 집합
  • A의 레벨 : 1
  • B, C의 레벨 : 2
  • D, E, F, G, H의 레벨 : 3
• 노드의 차수(degree) : 부(하위) 트리 갯수/간선수 (degree) = 각 노드가 지닌 가지의 수
  • A의 차수 = 2
  • B의 차수 = 3
  • C의 차수 = 2
• 트리의 차수(degree of tree) : 트리의 최대 차수
  • B가 최대 차수를 가짐 => 3
• 트리의 높이(height) : 루트 노드에서 가장 깊숙히 있는 노드의 깊이
  • 3

3) 트리의 기본적인 성질

• 노드가 N개인 트리는 항상 N-1개의 링크(link)를 가진다
• 트리에서, 루트에서 어떤 노드로 가는 경로는 유일하다. 또한 임의의 두 노드 간의 경로도 유일하다 (같은 노드를 두 번 이상 방문하지 않는 다는 조건 하에)

(2) 이진트리(Binary Tree)

1) 개념

• 이진 트리에서 각 노드는 최대 2개의 자식을 가진다.
• 각각의 자식 노드는 자신이 부모의 왼쪽 자식인지 오른쪽 자식인지가 지정된다.
  • 자식이 한 명인 경우에도 적용

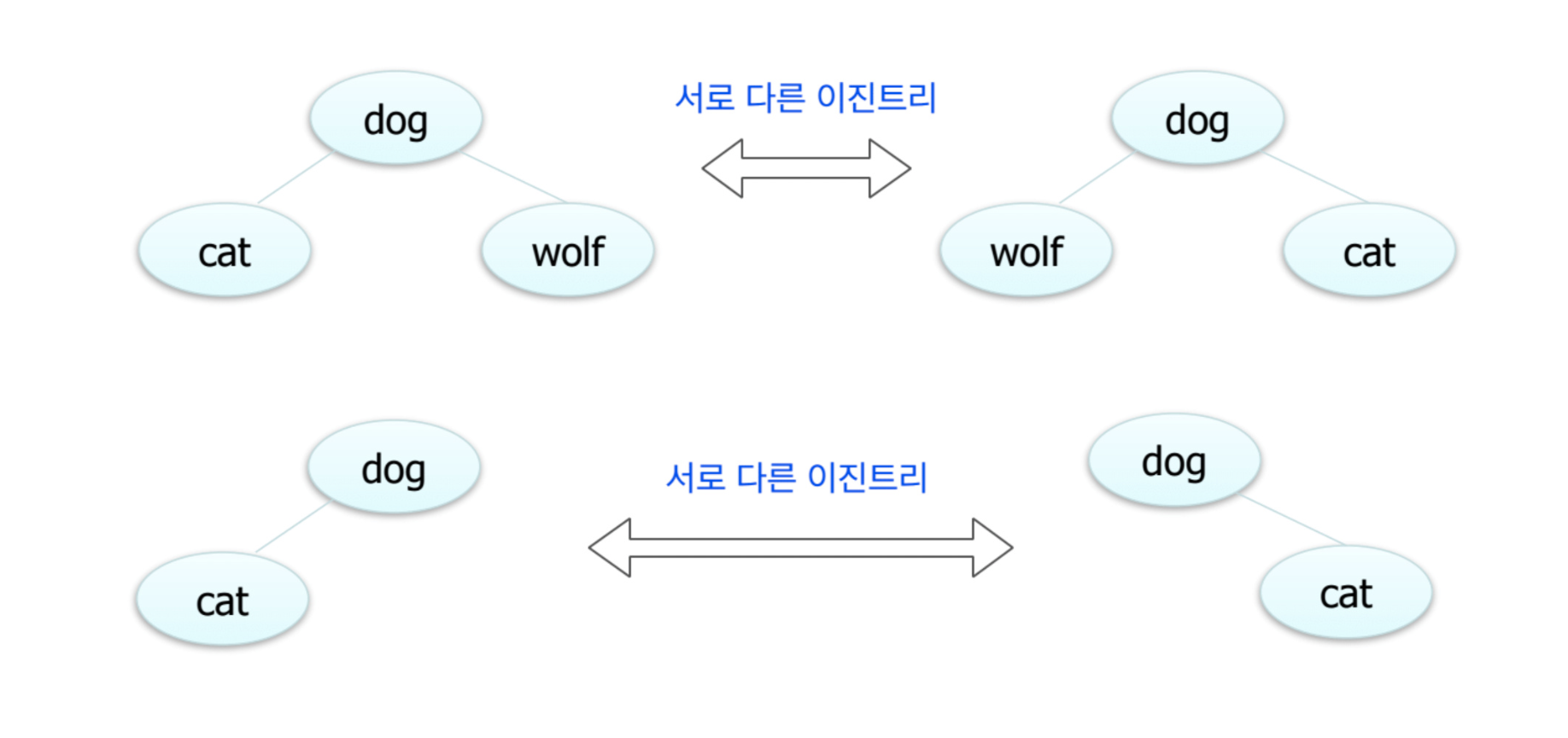
2) 이진 트리 종류

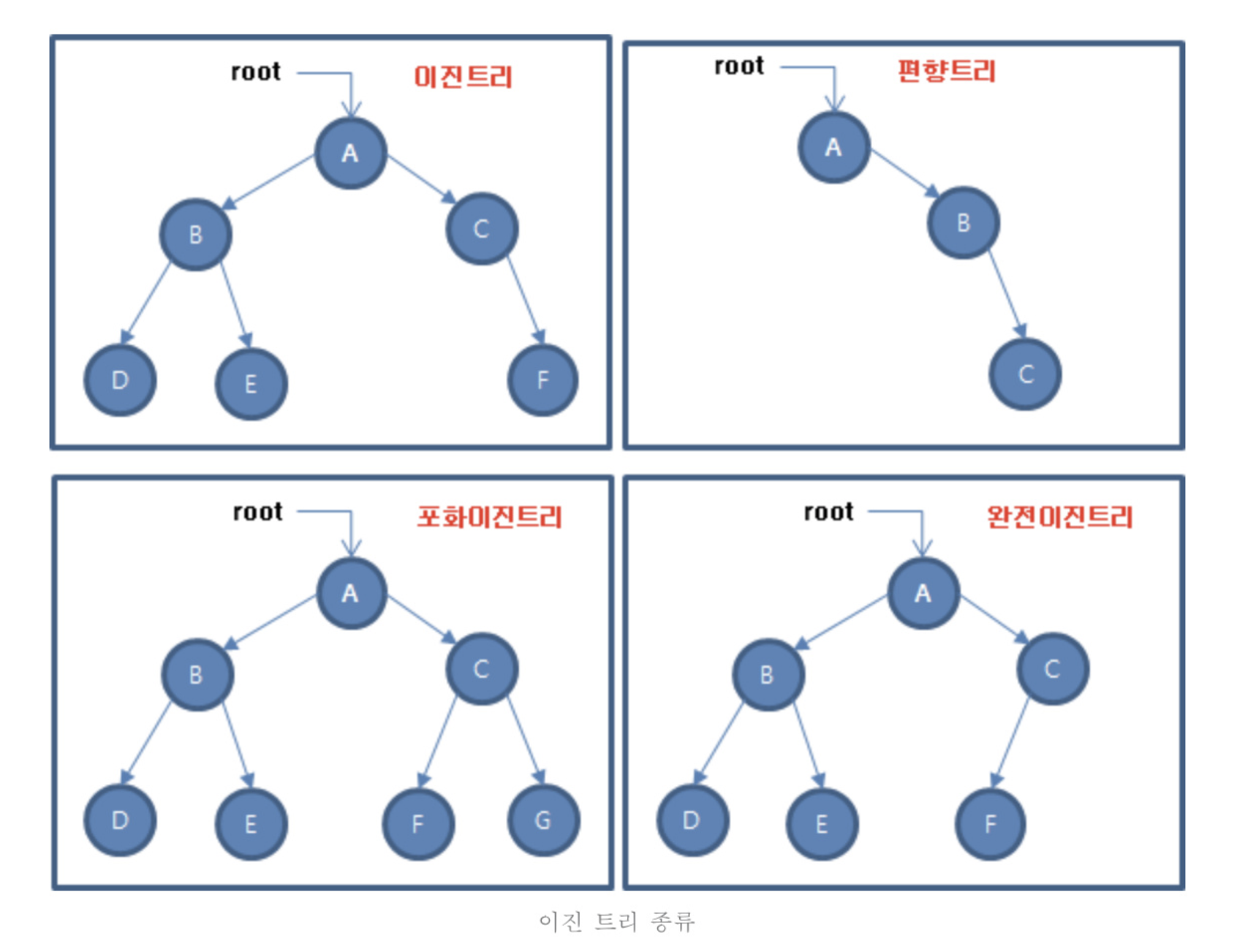
• 포화 이진 트리(full binary tree) : 모든 레벨에서 노드들이 모두 채워져 있는 트리
• 완전 이진트리(complete binary tree)
  • 마지막 레벨을 제외하고 노드가 모두 채워져 있는 트리
    • 마지막 레벨도 다 채워져 있을 수도 있음
  • 마지막 레벨도 오른쪽으로 연속된 몇개의 노드만 비어있을 수 있음

3) 이진트리 특징

• 높이가 h인 포화 이진 트리(full binary tree)는 \(2^h-1\)개의 노드를 가진다
• 노드가 N개인 포화(full) 혹은 완전(complete) 이진 트리의 높이는 \(O(logN)\)이다.
• 노드가 N개인 이진트리의 높이는 최악의 경우 \(O(N)\)이 될 수 있다.